OptiBlog by Luka Diktić
← Back Repo →

3D bin packing using a genetic algorithm

3D bin packinggenetic algorithmEMSDFTRC-2metaheuristics

TLDR

Motivation

Packing problems appear in the literature as early as the 1970s, first in 1D and 2D forms. Early approaches were simple heuristics like First-Fit and Best-Fit, while with increasing computing power the focus shifted more toward metaheuristic solutions (especially from the 1990s to today). Practical applications are common: logistics, warehousing, transport planning, manufacturing, and generally any system where we want to minimize the number of containers or maximize volume utilization.
This problem is NP-hard, so in practice approximation and heuristic approaches are often used.
What I find especially interesting is that the problem has been present in industry for a long time, yet it is still actively researched due to its complexity and practical importance.
This work focuses on the 3D variant with realistic details such as rotations and non-homogeneous containers.

Problem

We have a finite set of objects, where each object i is defined by dimensions (wᵢ, hᵢ, dᵢ). Each container b has dimensions (Wᵦ, Hᵦ, Dᵦ). The goal is to assign each object to a container and a position (and potentially a rotation) such that:

Objects can be orthogonally rotated, which is equivalent to permuting dimensions, so each object has up to 6 configurations.

Approach

The solution consists of two components:

  1. A genetic algorithm (GA) that searches the space of solutions (orders and orientations).
  2. A packing heuristic that, for a given chromosome, tries to construct a concrete layout in containers and returns how many containers are required.

In each GA iteration:

Solution encoding (chromosome)

An individual’s chromosome is a vector of length 2n + m:

Why real numbers in [0,1]?

Rotations are not encoded directly as {0..5}, but as a coefficient that is later mapped to one of the allowed rotations in the current container context.

Packing heuristic

Empty Maximal Spaces (EMS)

Free space in a container is represented by a list of EMS volumes: each EMS represents the largest rectangular empty block currently available in the container. After placing an object, the EMS list is updated:

  1. select an EMS that can fit the object,
  2. generate new EMS blocks based on the intersection of the object and the selected EMS,
  3. remove degenerate or redundant EMS blocks,
  4. optionally remove EMS blocks that cannot fit any remaining object.

In practice, the object is positioned in the back-bottom-left corner of the selected EMS, which limits the growth in the number of newly created EMS blocks and keeps the space compact.

EMS selection heuristics

I implemented and compared several heuristics:

DFTRC-2 is effectively a local search: for each object it checks all allowed rotations across all EMS blocks and selects the best option according to the distance criterion. In the actual packing step, the rotation stored in the chromosome is still used, so the chromosome continues to have a significant impact on the final outcome.

Genetic algorithm

Selection

I used elitism (e.g., 5% of the population stays untouched) and tournament selection:

Crossover

Crossover turned out to be unexpectedly sensitive because of the encoding:

Because of that, SBX and uniform approaches did not perform well (weak learning rate; the best individual was often obtained almost randomly). The best approach was one-point crossover:

Mutation

Mutation iterates through each gene and, with a small probability, replaces its value with a new one from [0,1]. I tested multiple mutation rates (1%, 5%, 10%) to find a balance between stability and exploration.

Fitness function

The simplest fitness would be:

However, if two solutions use the same number of containers, it helps to further distinguish packing quality. Therefore, the fitness also includes the relative fill of the least utilized container, e.g.:

Fitness = number of containers + (least utilized volume / container capacity)

This provides a finer grading between solutions that use the same number of containers. The problem is a minimization problem: the goal is to reduce fitness.

Results analysis

Stopping criterion

On simpler instances, the optimal solution appeared after only a few dozen generations, while on more complex instances there is fast early learning followed by stagnation after ~100 generations. As a practical stopping criterion I used 100 generations, and repeated each measurement 20 times.

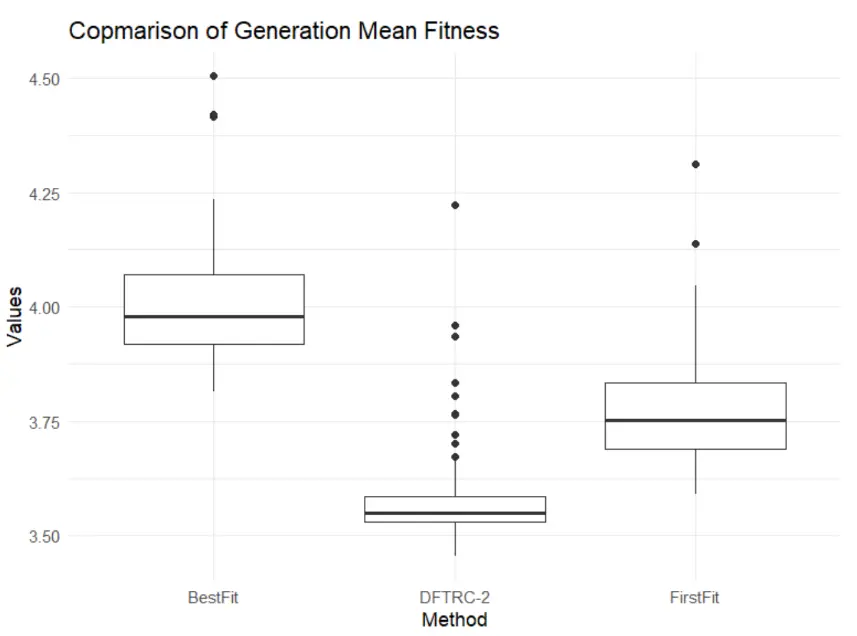
Comparison of packing heuristics

The packing heuristic has a major impact because evaluation constructs the full solution. In tests, DFTRC-2 clearly outperformed First-Fit and Best-Fit.
Interestingly, First-Fit performed better than Best-Fit, even though intuitively Best-Fit should often fill space better. In practice this depends on EMS dynamics and how choosing a smaller EMS affects future packing options.

Heuristic comparison

Comparison of mutation rates

I tested 1%, 5%, and 10% mutation:

Mutation comparison

Conclusion

Three-dimensional packing, while it may look trivial at first, is a very interesting and challenging optimization problem that has been relevant for decades. In this work I implemented a solution that combines:

The analysis showed that:

Further ideas

← Back Repo →